Technology powered by human expertise.
We're always working to grow your money—maximizing returns, minimizing taxes, and handling all the busywork. Every decision is guided by real experts focused on helping you build wealth over the long term.
-
Automated
We manage all the trading, rebalancing, reinvesting, and tax management for you, moves that make a big difference over decades. -
Personalized
We build an investing portfolio around what you want to accomplish, whether that’s retirement or simply building wealth. -
Diversified
Your money is invested across global markets and asset classes, a proven way to build wealth through all market cycles. -
Expert-managed
Our in-house Investing Team regularly monitors, analyzes, and updates portfolios to strengthen your investments.
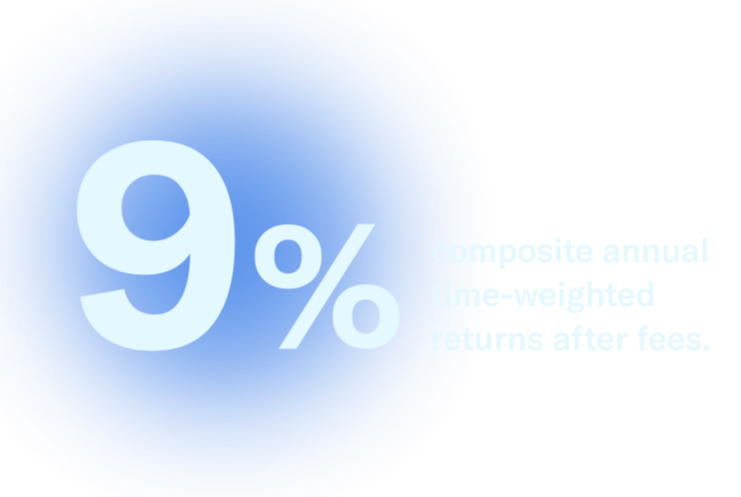
As of 12/31/2024, and inception date 9/7/2011. Composite annual time-weighted returns: 12.7% over 1 year, 7.9% over 5 years, and 7.8% over 10 years. Composite performance calculated based on the dollar-weighted average of actual client time-weighted returns for the Core portfolio at 90/10 allocation, net of fees, includes dividend reinvestment, and excludes the impact of cash flows. Performance not guaranteed, investing involves risk.
Investing that fits your needs.

Invest for retirement.
Traditional IRA, Roth IRA, SEP IRA, 401(k) rollover, and solo 401(k).

Invest for everything else.
Individual accounts, joint accounts, trust accounts.

Make your retirement more tax-efficient.
Open both an IRA and a taxable investing account, and we’ll coordinate them to help minimize tax liabilities and better grow your retirement savings.
A portfolio for every kind of investor.
Choose from portfolios ranging from broad global diversification to socially responsible to low-risk bonds to crypto—and we’ll handle the rest.
Want more personalization? We make it easy to customize your assets to fit your needs while still benefiting from our guidance and tax saving technology.

Investing optimized by tax smart technology
Our tax-loss harvesting helps lower your tax bill and your long-term returns. It works automatically to take advantage of market dips and keep you invested.
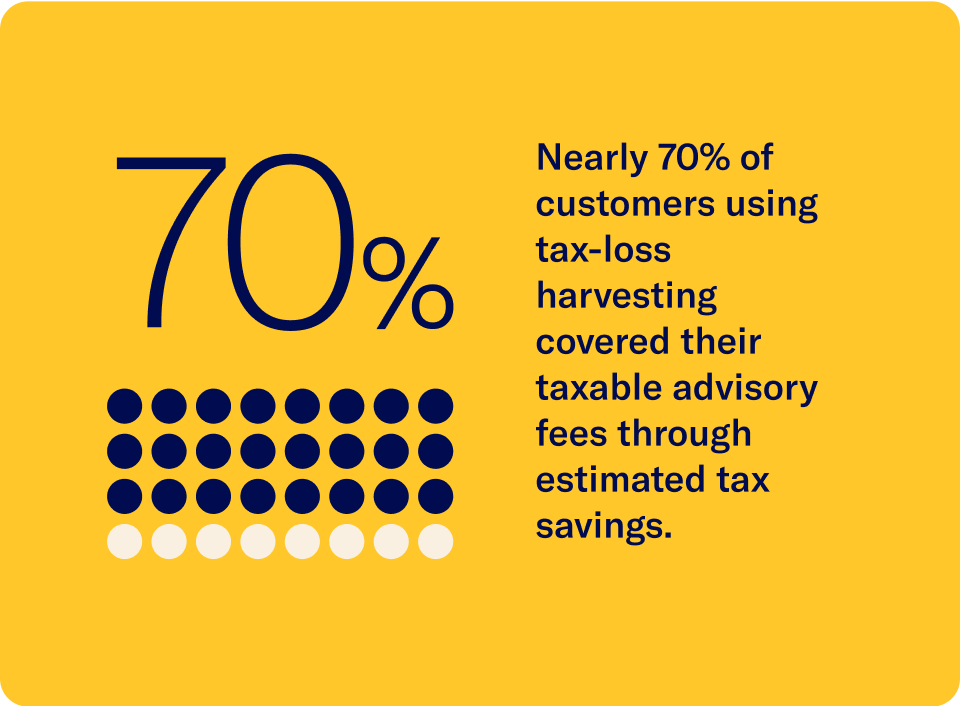
Plus, it could cover your investing fee.
Plus, it could cover your investing fee.
Based on 2022-2023. Tax Loss Harvesting (TLH) is not suitable for all investors. Consider your personal circumstances before deciding whether to utilize Betterment’s TLH feature. Fee coverage and estimated tax savings based on Betterment internal calculations. See more in disclosures.
-
Pay for a wedding
-
Save for education
-
Buy a home
-
Build wealth
Trusted to do what's right for your money.
As a fiduciary, we're legally bound to put your interests first when you invest.
-

$60+ Billion in assets
-

Nearly 1 million customers
Based on Betterment internal data as of 5/12/25. -
 Member of SIPC, which protects securities customers of its members up to $500,000 (including $250,000 for claims for cash). Explanatory brochure available upon request or at www.sipc.org.
Member of SIPC, which protects securities customers of its members up to $500,000 (including $250,000 for claims for cash). Explanatory brochure available upon request or at www.sipc.org. -

4.8 out of 5 stars
72k reviews
Weighted avg. app store rating as of 6.2.25 (reviews since: 9.10.10 Apple, 10.30.13 Google). See more.



