Betterment's asset location methodology
Intelligently applying asset location to a globally diversified portfolio is a complex, mathematically rigorous, and continuous undertaking.
TABLE OF CONTENTS
- Summary
- Part I: Introduction to Asset Location
- Part II: After-Tax Return—Deep Dive
- Part III: Asset Location Myths
- Part IV: TCP Methodology
- Part V: Monte Carlo on the Amazon—Betterment’s Testing Framework
- Part VI: Results
- Part VII: Special Considerations
- Addendum
Summary
Asset location is widely regarded as the closest thing there is to a "free lunch" in the wealth management industry.1 When investments are held in at least two types of accounts (out of three possible types: taxable, tax-deferred and tax-exempt), asset location provides the ability to deliver additional after-tax return potential, while maintaining the same level of risk.
Generally speaking, this benefit is achieved by placing the least tax-efficient assets in the accounts taxed most favorably, and the most tax-efficient assets in the accounts taxed least favorably, all while maintaining the desired asset allocation in the aggregate.
Part I: Introduction to Asset Location
Maximizing after-tax return on investments can be complex. Still, most investors know that contributing to tax-advantaged (or "qualified") accounts is a relatively straightforward way to pay less tax on their retirement savings. Millions of Americans wind up with some combination of IRAs and 401(k) accounts, both available in two types: traditional or Roth. Many will only save in a taxable account once they have maxed out their contribution limits for the qualified accounts. But while tax considerations are paramount when choosing which account to fund, less thought is given to the tax impact of which investments to then purchase across all accounts.
The tax profiles of the three account types (taxable, traditional, and Roth) have implications for what to invest in, once the account has been funded. Choosing wisely can significantly improve the after-tax value of one’s savings, when more than one account is in the mix.
Almost universally, such investors can benefit from a properly executed asset location strategy. The idea behind asset location is fairly straightforward. Certain investments generate their returns in a more tax-efficient manner than others. Certain accounts shelter investment returns from tax better than others. Placing, or "locating" less tax-efficient investments in tax-sheltered accounts could increase the after-tax value of the overall portfolio.
Allocate First, Locate Second
Let’s start with what asset location isn’t. All investors must select a mix of stocks and bonds, finding an appropriate balance of risk and expected potential return, in line with their goals. One common goal is retirement, in which case, the mix of assets should be tailored to match the investor’s time horizon. This initial determination is known as "asset allocation," and it comes first.
When investing in multiple accounts, it is common for investors to simply recreate their desired asset allocation in each account. If each account, no matter the size, holds the same assets in the same proportions, adding up all the holdings will also match the desired asset allocation. If all these funds, however scattered, are invested towards the same goal, this is the right result. The aggregate portfolio is the one that matters, and it should track the asset allocation selected for the common goal.
Portfolio Managed Separately in Each Account
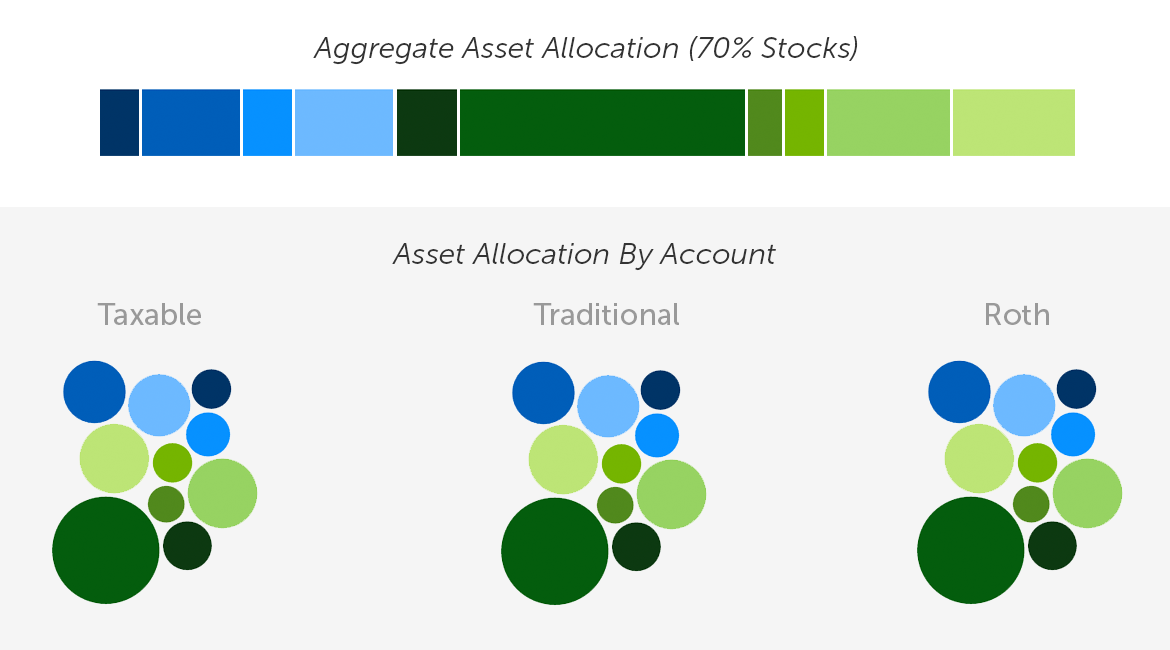
Enter asset location, which can only be applied once a desired asset allocation is selected. Each asset’s after-tax return is considered in the context of every available account. The assets are then arranged (unequally) across all coordinated accounts to help maximize the after-tax performance of the overall portfolio.
Same Portfolio Overall—With Asset Location
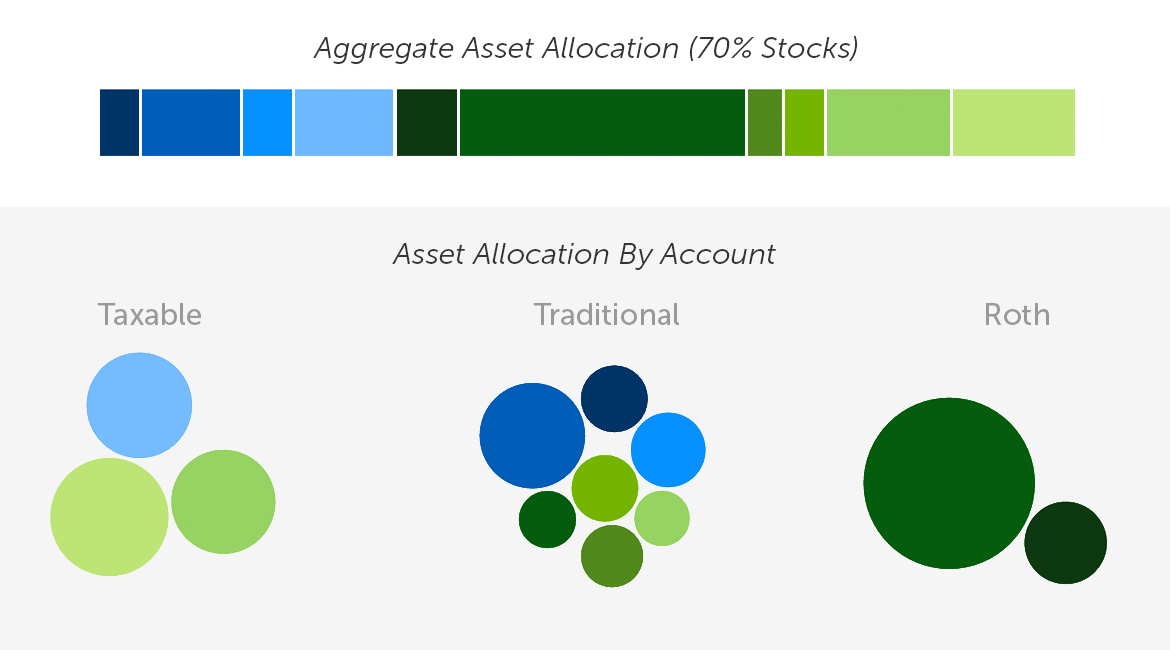
To help conceptualize asset location, consider a team of runners. Some runners compete better on a track than a cross-country dirt path, as compared to their more versatile teammates. Similarly, certain asset classes can benefit more than others from the tax-efficient "terrain" of a qualified account.
Asset allocation determines the composition of the team, and the overall portfolio’s after-tax return is a team effort. Asset location then seeks to match up asset and environment in a way that maximizes the overall result over time, while keeping the composition of the team intact.
TCP vs. TDF
The primary appeal of a target-date fund (TDF) is the "set it and forget it" simplicity with which it allows investors to select and maintain a diversified asset allocation, by purchasing only one fund. That simplicity comes at a price—because each TDF is a single, indivisible security, it cannot unevenly distribute its underlying assets across multiple accounts, and thus cannot deliver the additional after-tax returns of asset location.
In particular, participants who are locked into 401(k) plans without automated management may find that a cheap TDF is still their best "hands off" option (plus, a TDF’s ability to satisfy the Qualified Default Investment Alternative (QDIA) requirement under ERISA ensures its baseline survival under current law).
Participants in a Betterment at Work plan can already enable Betterment’s Tax-Coordinated Portfolio feature (“TCP”) to manage a single portfolio across their 401(k), IRAs and taxable accounts they individually have with Betterment, designed to squeeze additional after-tax returns from their aggregate long-term savings.
Automated asset location (when integrated with automated asset allocation) replicates what makes a TDF so appealing, but effectively amounts to a "TDF 2.0"—a continuously managed portfolio, but one that can straddle multiple accounts for tax benefits.
Next, we dive into the complex dynamics that need to be considered when seeking to optimize the after-tax return of a diversified portfolio.
Part II: After-Tax Return—Deep Dive
A good starting point for a discussion of investment taxation is the concept of "tax drag." Tax drag is the portion of the return that is lost to tax on an annual basis. In particular, funds pay dividends, which are taxed in the year they are received.
However, there is no annual tax in qualified accounts, also sometimes known as "tax-sheltered accounts." Therefore, placing assets that pay a substantial amount of dividends into a qualified account, rather than a taxable account, "shelters" those dividends, and reduces tax drag. Reducing the tax drag of the overall portfolio is one way that asset location improves the portfolio’s potential after-tax return.
Importantly, investments are also subject to tax at liquidation, both in the taxable account, and in a traditional IRA (where tax is deferred). However, "tax drag", as that term is commonly used, does not include liquidation tax. So while the concept of "tax drag" is intuitive, and thus a good place to start, it cannot be the sole focus when looking to help minimize taxes.
What is "Tax Efficiency"
A closely related term is "tax efficiency" and this is one that most discussions of asset location will inevitably focus on. A tax-efficient asset is one that has minimal "tax drag." Prioritizing assets on the basis of tax efficiency allows for asset location decisions to be made following a simple, rule-based approach.
Both "tax drag" and "tax efficiency" are concepts pertaining to taxation of returns in a taxable account. Therefore, we first consider that account, where the rules are most elaborate. With an understanding of these rules, we can layer on the impact of the two types of qualified accounts.
Returns in a Taxable Account
There are two types of investment income, and two types of applicable tax rates.
Two types of investment tax rates. All investment income in a taxable brokerage account is subject to one of two rate categories (with material exceptions noted). For simplicity, and to keep the analysis universal, this section only addresses federal tax (state tax is considered when testing for performance).
- Ordinary rate: For most, this rate mirrors the marginal tax bracket applicable to earned income (primarily wages reported on a W-2).
- Preferential rate: This more favorable rate ranges from 15% to 20% for most investors.
For especially high earners, both rates are subject to an additional tax of 3.8%.
Two types of investment returns. Investments generate returns in two ways: by appreciating in value, and by making cash distributions.
- Capital gains: When an investment is sold, the difference between the proceeds and the tax basis (generally, the purchase price) is taxed as capital gains. If held for longer than a year, this gain is treated as long-term capital gains (LTCG) and taxed at the preferential rate. If held for a year or less, the gain is treated as short-term capital gains (STCG), and taxed at the ordinary rate. Barring unforeseen circumstances, passive investors should be able to avoid STCG entirely. Betterment’s automated account management seeks to avoid STCG when possible,4 and the rest of this paper assumes only LTCG on liquidation of assets.
- Dividends: Bonds pay interest, which is taxed at the ordinary rate, whereas stocks pay dividends, which are taxed at the preferential rate (both subject to the exceptions below). An exchange-traded fund (ETF) pools the cash generated by its underlying investments, and makes payments that are called dividends, even if some or all of the source was interest. These dividends inherit the tax treatment of the source payments. This means that, generally, a dividend paid by a bond ETF is taxed at the ordinary rate, and a dividend paid by a stock ETF is taxed at the preferential rate.
- Qualified Dividend Income (QDI): There is an exception to the general rule for stock dividends. Stock dividends enjoy preferential rates only if they meet the requirements of qualified dividend income (QDI). Key among those requirements is that the company issuing the dividend must be a U.S. corporation (or a qualified foreign corporation). A fund pools dividends from many companies, only some of which may qualify for QDI. To account for this, the fund assigns itself a QDI percentage each year, which the custodian uses to determine the portion of the fund’s dividends that are eligible for the preferential rate. For stock funds tracking a U.S. index, the QDI percentage is typically 100%. However, funds tracking a foreign stock index will have a lower QDI percentage, sometimes substantially. For example, VWO, Vanguard’s Emerging Markets Stock ETF, had a QDI percentage of 38% in 2015, which means that 38% of its dividends for the year were taxed at the preferential rate, and 62% were taxed at the ordinary rate.
- Tax-exempt interest: There is also an exception to the general rule for bonds. Certain bonds pay interest that is exempt from federal tax. Primarily, these are municipal bonds, issued by state and local governments. This means that an ETF which holds municipal bonds will pay a dividend that is subject to 0% federal tax—even better than the preferential rate.
The table below summarizes these interactions. Note that this section does not consider tax treatment for those in a marginal tax bracket of 15% and below. These taxpayers are addressed in "Special Considerations."
| Dividends (taxed annually) | Capital Gains (taxed when sold) | |
|---|---|---|
| Ordinary Rate |
Most bonds |
Any security held for a year or less (STCG) |
| Preferential Rate | QDI stocks (domestic and some foreign) | Any security held for more than a year (LTCG) |
| No Tax | Municipal bonds | Any security transferred upon death or donated to charity |
The impact of rates is obvious: The higher the rate, the higher the tax drag. Equally important is timing. The key difference between dividends and capital gains is that the former are taxed annually, contributing to tax drag, whereas tax on the latter is deferred.
Tax deferral is a powerful driver of after-tax return, for the simple reason that the savings, though temporary, can be reinvested in the meantime, and compounded. The longer the deferral, the more valuable it is.
Putting this all together, we arrive at the foundational piece of conventional wisdom, where the most basic approach to asset location begins and ends:
- Bond funds are expected to generate their return entirely through dividends, taxed at the ordinary rate. This return benefits neither from the preferential rate, nor from tax deferral, making bonds the classic tax-inefficient asset class. These go in your qualified account.
- Stock funds are expected to generate their return primarily through capital gains. This return benefits both from the preferential rate, and from tax deferral. Stocks are therefore the more tax-efficient asset class. These go in your taxable account.
Tax-Efficient Status: It’s Complicated
Reality gets messy rather quickly, however. Over the long term, stocks are expected to grow faster than bonds, causing the portfolio to drift from the desired asset allocation. Rebalancing may periodically realize some capital gains, so we cannot expect full tax deferral on these returns (although if cash flows exist, investing them intelligently can potentially reduce the need to rebalance via selling).
Furthermore, stocks do generate some return via dividends. The expected dividend yield varies with more granularity. Small cap stocks pay relatively little (these are growth companies that tend to reinvest any profits back into the business) whereas large cap stocks pay more (as these are mature companies that tend to distribute profits). Depending on the interest rate environment, stock dividends can exceed those paid by bonds.
International stocks pay dividends too, and complicating things further, some of those dividends will not qualify as QDI, and will be taxed at the ordinary rate, like bond dividends (especially emerging markets stock dividends).
Returns in a Tax-Deferred Account (TDA)
Compared to a taxable account, a TDA is governed by straightforward rules. However, earning the same return in a TDA involves trade-offs which are not intuitive. Applying a different time horizon to the same asset can swing our preference between a taxable account and a TDA.Understanding these dynamics is crucial to appreciating why an optimal asset location methodology cannot ignore liquidation tax, time horizon, and the actual composition of each asset’s expected return.Although growth in a traditional IRA or traditional 401(k) is not taxed annually, it is subject to a liquidation tax. All the complexity of a taxable account described above is reduced to two rules. First, all tax is deferred until distributions are made from the account, which should begin only in retirement. Second, all distributions are taxed at the same rate, no matter the source of the return.
The rate applied to all distributions is the higher ordinary rate, except that the additional 3.8% tax will not apply to those whose tax bracket in retirement would otherwise be high enough.2
First, we consider income that would be taxed annually at the ordinary rate (i.e. bond dividends and non-QDI stock dividends). The benefit of shifting these returns to a TDA is clear. In a TDA, these returns will eventually be taxed at the same rate, assuming the same tax bracket in retirement. But that tax will not be applied until the end, and compounding due to deferral can only have a positive impact on the after-tax return, as compared to the same income paid in a taxable account.3
In particular, the risk is that LTCG (which we expect plenty of from stock funds) will be taxed like ordinary income. Under the basic assumption that in a taxable account, capital gains tax is already deferred until liquidation, favoring a TDA for an asset whose only source of return is LTCG is plainly harmful. There is no benefit from deferral, which you would have gotten anyway, and only harm from a higher tax rate. This logic supports the conventional wisdom that stocks belong in the taxable account. First, as already discussed, stocks do generate some return via dividends, and that portion of the return will benefit from tax deferral. This is obviously true for non-QDI dividends, already taxed as ordinary income, but QDI can benefit too. If the deferral period is long enough, the value of compounding will offset the hit from the higher rate at liquidation.
Second, it is not accurate to assume that all capital gains tax will be deferred until liquidation in a taxable account. Rebalancing may realize some capital gains "prematurely" and this portion of the return could also benefit from tax deferral.
Placing stocks in a TDA is a trade-off—one that must weigh the potential harm from negative rate arbitrage against the benefit of tax deferral. Valuing the latter means making assumptions about dividend yield and turnover. On top of that, the longer the investment period, the more tax deferral is worth. Kitces demonstrates that a dividend yield representing 25% of total return (at 100% QDI), and an annual turnover of 10%, could swing the calculus in favor of holding the stocks in a TDA, assuming a 30-year horizon.4 For foreign stocks with less than perfect QDI, we would expect the tipping point to come sooner.
Returns in a Tax-Exempt Account (TEA)
Investments in a Roth IRA or Roth 401(k) grow tax free, and are also not taxed upon liquidation. Since it eliminates all possible tax, a TEA presents a particularly valuable opportunity for maximizing after-tax return. The trade-off here is managing opportunity cost—every asset does better in a TEA, so how best to use its precious capacity?
Clearly, a TEA is the most favorably taxed account. Conventional wisdom thus suggests that if a TEA is available, we use it to first place the least tax-efficient assets. But that approach is wrong.
Everything Counts in Large Amounts—Why Expected Return Matters
The powerful yet simple advantage of a TEA helps illustrate the limitation of focusing exclusively on tax efficiency when making location choices. Returns in a TEA escape all tax, whatever the rate or timing would have been, which means that an asset’s expected after-tax return equals its expected total return.
When both a taxable account and a TEA are available, it may be worth putting a high-growth, low-dividend stock fund into the TEA, instead of a bond fund, even though the stock fund is vastly more tax-efficient. Similar reasoning can apply to placement in a TDA as well, as long as the tax-efficient asset has a large enough expected return, and presents some opportunity for tax deferral (i.e., some portion of the return comes from dividends).
Part III: Asset Location Myths
Urban Legend 1: Asset location is a one-time process. Just set it and forget it.
While an initial location may add some value, doing it properly is a continuous process, and will require adjustments in response to changing conditions. Note that overlaying asset location is not a deviation from a passive investing philosophy, because optimizing for location does not mean changing the overall asset allocation (the same goes for tax loss harvesting).
Other things that will change, all of which should factor into an optimal methodology: expected returns (both the risk-free rate, and the excess return), dividend yields, QDI percentages, and most importantly, relative account balances. Contributions, rollovers, and conversions can increase qualified assets relative to taxable assets, continuously providing more room for additional optimization.
Urban Legend 2: Taking advantage of asset location means you should contribute more to a particular qualified account than you otherwise would.
Definitely not! Asset location should play no role in deciding which accounts to fund. It optimizes around account balances as it finds them, and is not concerned with which accounts should be funded in the first place. Just because the presence of a TEA makes asset location more valuable, does not mean you should contribute to a TEA, as opposed to a TDA. That decision is primarily a bet on how your tax rate today will compare to your tax rate in retirement. To hedge, some may find it optimal to make contributions to both a TDA and TEA (this is called "tax diversification"). While these decisions are out of scope for this paper, Betterment’s retirement planning tools can help clients with these choices.
Urban Legend 3: Asset location has very little value if one of your accounts is relatively small.
It depends. Asset location will not do much for investors with a very small taxable balance and a relatively large balance in only one type of qualified account, because most of the overall assets are already sheltered. However, a large taxable balance and a small qualified account balance (especially a TEA balance) presents a better opportunity. Under these circumstances, there may be room for only the least tax-efficient, highest-return assets in the qualified account. Sheltering a small portion of the overall portfolio can deliver a disproportionate amount of value.
Urban Legend 4: Asset location has no value if you are investing in both types of qualified accounts, but not in a taxable account.
A TEA offers significant advantages over a TDA. Zero tax is better than a tax deferred until liquidation. While tax efficiency (i.e. annual tax drag) plays no role in these location decisions, expected returns and liquidation tax do. The assets we expect to grow the most should be placed in a TEA, and doing so will plainly increase the overall after-tax return. There is an additional benefit as well. Required minimum distributions (RMDs) apply to TDAs but not TEAs. Shifting expected growth into the TEA, at the expense of the TDA, will mean lower RMDs, giving the investor more flexibility to control taxable income down the road. In other words, a lower balance in the TDA can mean lower tax rates in retirement, if higher RMDs would have pushed the retiree into a higher bracket. This potential benefit is not captured in our results.
Urban Legend 5: Bonds always go in the IRA.
Possibly, but not necessarily. This commonly asserted rule is a simplification, and will not be optimal under all circumstances. It is discussed at more length below.
Existing Approaches to Asset Location: Advantages and Limitations
Optimizing for After-Tax Return While Maintaining Separate Portfolios
One approach to increasing after-tax return on retirement savings is to maintain a separate, standalone portfolio in each account with roughly the same level of risk-adjusted return, but tailoring each portfolio somewhat to take advantage of the tax profile of the account. Effectively, this means that each account separately maintains the desired exposure to stocks, while substituting certain asset classes for others.
Generally speaking, managing a fully diversified portfolio in each account means that there is no way to avoid placing some assets with the highest expected return in the taxable account.
This approach does include a valuable tactic, which is to differentiate the high-quality bonds component of the allocation, depending on the account they are held in. The allocation to the component is the same in each account, but in a taxable account, it is represented by municipal bonds which are exempt from federal tax , and in a qualified account, by taxable investment grade bonds .
This variation is effective because it takes advantage of the fact that these two asset classes have very similar characteristics (expected returns, covariance and risk exposures) allowing them to play roughly the same role from an asset allocation perspective. Municipal bonds are highly tax-efficient due to their federal tax-exempt interest income, making them particularly compelling for a taxable account. Taxable investment grade bonds have significant tax drag, and work best in a qualified account. Betterment has applied this substitution since 2014.
The Basic Priority List
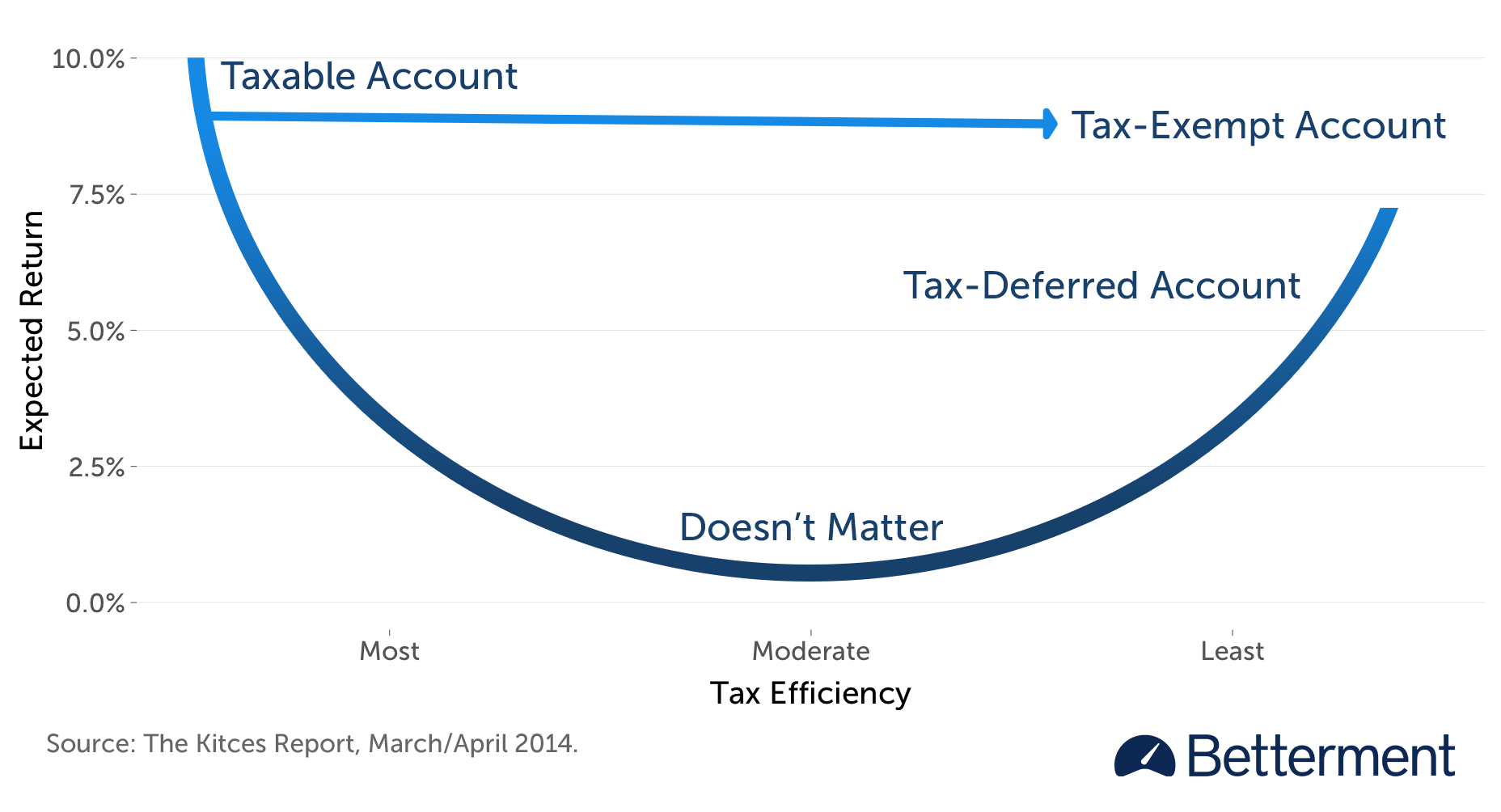
Gobind Daryanani and Chris Cordaro sought to balance considerations around tax efficiency and expected return, and illustrated that when both are very low, location decisions with respect to those assets have very limited impact.5 That study inspired Michael Kitces, who leverages its insights into a more sophisticated approach to building a priority list.6 To visually capture the relationship between the two considerations, Kitces bends the one-dimensional list into a "smile."
Asset Location Priority List
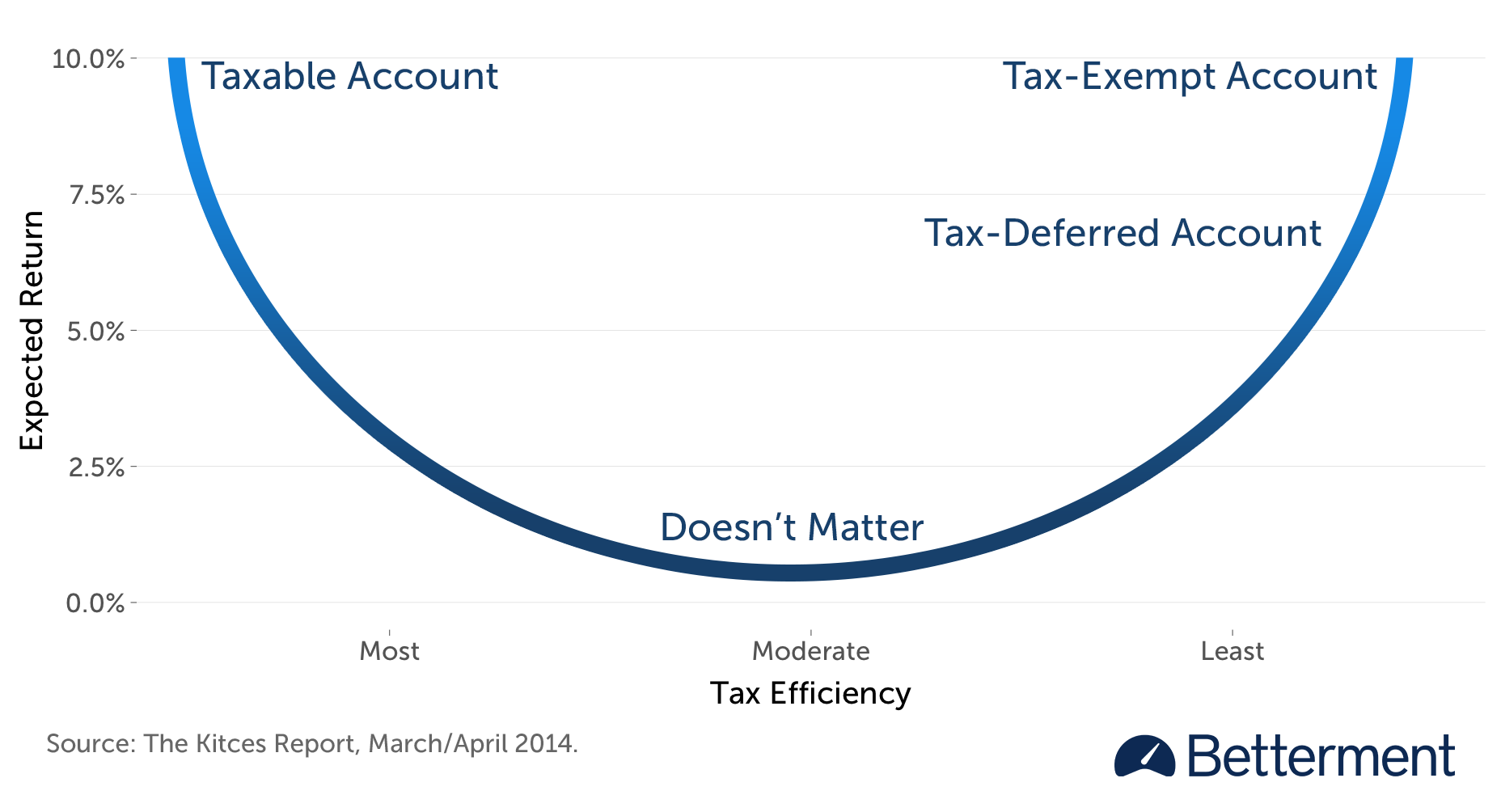
Assets with a high expected return that are also very tax-efficient go in the taxable account. Assets with a high expected return that are also very tax-inefficient go in the qualified accounts, starting with the TEA. The "smile" guides us in filling the accounts from both ends simultaneously, and by the time we get to the middle, whatever decisions we make with respect to those assets just "don’t matter" much.
However, Kitces augments the graph in short order, recognizing that the basic "smile" does not capture a third key consideration—the impact of liquidation tax. Because capital gains will eventually be realized in a taxable account, but not in a TEA, even a highly tax-efficient asset might be better off in a TEA, if its expected return is high enough. The next iteration of the "smile" illustrates this preference.
Asset Location Priority List with Limited High Return Inefficient Assets
Part IV: TCP Methodology
There is no one-size-fits-all asset location for every set of inputs. Some circumstances apply to all investors, but shift through time—the expected return of each asset class (which combines separate assumptions for the risk-free rate and the excess return), as well as dividend yields, QDI percentages, and tax laws. Other circumstances are personal—which accounts the client has, the relative balance of each account, and the client’s time horizon.
Solving for multiple variables while respecting defined constraints is a problem that can be effectively solved by linear optimization. This method is used to maximize some value, which is represented by a formula called an "objective function." What we seek to maximize is the after-tax value of the overall portfolio at the end of the time horizon.
We get this number by adding together the expected after-tax value of every asset in the portfolio, but because each asset can be held in more than one account, each portion must be considered separately, by applying the tax rules of that account. We must therefore derive an account-specific expected after-tax return for each asset.
Deriving Account-Specific After-Tax Return
To define the expected after-tax return of an asset, we first need its total return (i.e., before any tax is applied). The total return is the sum of the risk-free rate (same for every asset) and the excess return (unique to every asset). Betterment derives excess returns using the Black-Litterman model as a starting point. This common industry method involves analyzing the global portfolio of investable assets and their proportions, and using them to generate forward-looking expected returns for each asset class.
Next, we must reduce each total return into an after-tax return.7 The immediate problem is that for each asset class, the after-tax return can be different, depending on the account, and for how long it is held.
- In a TEA, the answer is simple—the after-tax return equals the total return—no calculation necessary.
- In a TDA, we project growth of the asset by compounding the total return annually. At liquidation, we apply the ordinary rate to all of the growth.8 We use what is left of the growth after taxes to derive an annualized return, which is our after-tax return.
- In a taxable account, we need to consider the dividend and capital gain component of the total return separately, with respect to both rate and timing. We project growth of the asset by taxing the dividend component annually at the ordinary rate (or the preferential rate, to the extent that it qualifies as QDI) and adding back the after-tax dividend (i.e., we reinvest it). Capital gains are deferred, and the LTCG is fully taxed at the preferential rate at the end of the period. We then derive the annualized return based on the after-tax value of the asset.9
Note that for both the TDA and taxable calculations, time horizon matters. More time means more value from deferral, so the same total return can result in a higher annualized after-tax return. Additionally, the risk-free rate component of the total return will also depend on the time horizon, which affects all three accounts.
Because we are accounting for the possibility of a TEA, as well, we actually have three distinct after-tax returns, and thus each asset effectively becomes three assets, for any given time horizon (which is specific to each Betterment customer).
The Objective Function
To see how this comes together, we first consider an extremely simplified example. Let’s assume we have a taxable account, both a traditional and Roth account, with $50,000 in each one, and a 30-year horizon. Our allocation calls for only two assets: 70% equities (stocks) and 30% fixed income (bonds). With a total portfolio value of $150,000, we need $105,000 of stocks and $45,000 of bonds.
1. These are constants whose value we already know (as derived above).
req,tax is the after-tax return of stocks in the taxable account, over 30 years
req,trad is the after-tax return of stocks in the traditional account, over 30 years
req,roth is the after-tax return of stocks in the Roth account, over 30 years
rfi,tax is the after-tax return of bonds in the taxable account, over 30 years
rfi,trad is the after-tax return of bonds in the traditional account, over 30 years
rfi,roth is the after-tax return of bonds in the Roth account, over 30 years
2. These are the values we are trying to solve for (called "decision variables").
xeq,tax is the amount of stocks we will place in the taxable account
xeq,trad is the amount of stocks we will place in the traditional account
xeq,roth is the amount of stocks we will place in the Roth account
xfi,tax is the amount of bonds we will place in the taxable account
xfi,trad is the amount of bonds we will place in the traditional account
xfi,roth is the amount of bonds we will place in the Roth account
3. These are the constraints which must be respected. All positions for each asset must add up to what we have allocated to the asset overall. All positions in each account must add up to the available balance in each account.
xeq,tax + xeq,trad + xeq,roth = 105,000
xfi,tax + xfi,trad + xfi,roth = 45,000
xeq,tax + xfi,tax = 50,000
xeq,trad + xfi,trad = 50,000
xeq,roth + xfi,roth = 50,000
4. This is the objective function, which uses the constants and decision variables to express the after-tax value of the entire portfolio, represented by the sum of six terms (the after-tax value of each asset in each of the three accounts).
maxx req,taxxeq,tax + req,tradxeq,trad + req,rothxeq,roth + rfi,taxxfi,tax + rfi,tradxfi,trad + rfi,rothxfi,roth
Linear optimization turns all of the above into a complex geometric representation, and mathematically closes in on the optimal solution. It assigns values for all decision variables in a way that maximizes the value of the objective function, while respecting the constraints. Accordingly, each decision variable is a precise instruction for how much of which asset to put in each account. If a variable comes out as zero, then that particular account will contain none of that particular asset.
An actual Betterment portfolio can potentially have twelve asset classes,15 depending on the allocation. That means TCP must effectively handle up to 36 "assets," each with its own after-tax return. However, the full complexity behind TCP goes well beyond increasing assets from two to twelve.
Updated constants and constraints will trigger another part of the optimization, which determines what TCP is allowed to sell, in order to move an already coordinated portfolio toward the newly optimal asset location, while minimizing taxes. Reshuffling assets in a TDA or TEA is "free" in the sense that no capital gains will be realized.10 In the taxable account, however, TCP will attempt to move as close as possible towards the optimal asset location without realizing capital gains.
Expected returns will periodically be updated, either because the risk-free rate has been adjusted, or because new excess returns have been derived via Black-Litterman.
Future cash flows may be even more material. Additional funds in one or more of the accounts could significantly alter the constraints which define the size of each account, and the target dollar allocation to each asset class. Such events (including dividend payments, subject to a de minimis threshold) will trigger a recalculation, and potentially a reshuffling of the assets.
Cash flows, in particular, can be a challenge for those managing their asset location manually. Inflows to just one account (or to multiple accounts in unequal proportions) create a tension between optimizing asset location and maintaining asset allocation, which is hard to resolve without mathematical precision.
To maintain the overall asset allocation, each position in the portfolio must be increased pro-rata. However, some of the additional assets we need to buy "belong" in other accounts from an asset location perspective, even though new cash is not available in those accounts. If the taxable account can only be partially reshuffled due to built-in gains, we must choose either to move farther away from the target allocation, or the target location.11
With linear optimization, our preferences can be expressed through additional constraints, weaving these considerations into the overall problem. When solving for new cash flows, TCP penalizes allocation drift higher than it does location drift.
Against this background, it is important to note that expected returns (the key input into TCP, and portfolio management generally) are educated guesses at best. No matter how airtight the math, reasonable people will disagree on the "correct" way to derive them, and the future may not cooperate, especially in the short-term. There is no guarantee that any particular asset location will add the most value, or even any value at all. But given decades, the likelihood of this outcome grows.
Part V: Monte Carlo—Betterment’s Testing Framework
To test the output of the linear optimization method, we turned to a Monte Carlo testing framework,12 built entirely in-house by Betterment’s experts. The forward-looking simulations model the behavior of the TCP strategy down to the individual lot level. We simulate the paths of these lots, accounting for dividend reinvestment, rebalancing, and taxation.
The simulations applied Betterment’s rebalancing methodology, which corrects drift from the target asset allocation in excess of 3% once the account balance meets or exceeds the required threshold, but stops short of realizing STCG, when possible.
Betterment’s management fees were assessed in all accounts, and ongoing taxes were paid annually from the taxable account. All taxable sales first realized available losses before touching LTCG.
The simulations assume no additional cash flows other than dividends. This is not because we do not expect them to happen. Rather, it is because making assumptions around these very personal circumstances does nothing to isolate the benefit of TCP specifically. Asset location is driven by the relative sizes of the accounts, and cash flows will change these ratios, but the timing and amount is highly specific to the individual.19 Avoiding the need to make specific assumptions here helps keep the analysis more universal. We used equal starting balances for the same reason.13
For every set of assumptions, we ran each market scenario while managing each account as a standalone (uncoordinated) Betterment portfolio as the benchmark.14 We then ran the same market scenarios with TCP enabled. In both cases, we calculated the after-tax value of the aggregate portfolio after full liquidation at the end of the period.15 Then, for each market scenario, we calculated the after-tax annualized internal rates of return (IRR) and subtracted the benchmark IRR from the TCP IRR. That delta represents the incremental tax alpha of TCP for that scenario. The median of those deltas across all market scenarios is the estimated tax alpha we present below for each set of assumptions.
Part VI: Results
More Bonds, More Alpha
A higher allocation to bonds leads to a dramatically higher benefit across the board. This makes sense—the heavier your allocation to tax-inefficient assets, the more asset location can do for you. To be extremely clear: this is not a reason to select a lower allocation to stocks! Over the long-term, we expect a higher stock allocation to return more (because it’s riskier), both before, and after tax. These are measurements of the additional return due to TCP, which say nothing about the absolute return of the asset allocation itself.
Conversely, a very high allocation to stocks shows a smaller (though still real) benefit. However, younger customers invested this aggressively should gradually reduce risk as they get closer to retirement (to something more like 50% stocks). Looking to a 70% stock allocation is therefore an imperfect but reasonable way to generalize the value of the strategy over a 30-year period.
More Roth, More Alpha
Another pattern is that the presence of a Roth makes the strategy more valuable. This also makes sense—a taxable account and a TEA are on opposite ends of the "favorably taxed" spectrum, and having both presents the biggest opportunity for TCP’s "account arbitrage." But again, this benefit should not be interpreted as a reason to contribute to a TEA over a TDA, or to shift the balance between the two via a Roth conversion. These decisions are driven by other considerations. TCP’s job is to optimize the relative balances as it finds them.
Enabling TCP On Existing Taxable Accounts
TCP should be enabled before the taxable account is funded, meaning that the initial location can be optimized without the need to sell potentially appreciated assets. A Betterment customer with an existing taxable account who enables TCP should not expect the full incremental benefit, to the extent that assets with built-in capital gains need to be sold to achieve the optimal location.
This is because TCP conservatively prioritizes avoiding a certain tax today, over potentially reducing tax in the future. However, the optimization is performed every time there is a deposit (or dividend) to any account. With future cash flows, the portfolio will move closer to whatever the optimal location is determined to be at the time of the deposit.
Part VII: Special Considerations
Low Bracket Taxpayers: Beware
Taxation of investment income is substantially different for those who qualify for a marginal tax bracket of 15% or below. To illustrate, we have modified the chart from Part II to apply to such low bracket taxpayers.
| Dividends | Capital Gains | |
|---|---|---|
| Ordinary Rate | N/A | Any security held for a year or less (STCG) |
| Preferential Rate | N/A | N/A |
| No Tax | Qualified dividends from any security are not taxed | Any security held for a year or more is not taxed (LTCG) |
TCP is not designed for these investors. Optimizing around this tax profile would reverse many assumptions behind TCP’s methodology. Municipal bonds no longer have an advantage over other bond funds. The arbitrage opportunity between the ordinary and preferential rate is gone. In fact, there’s barely tax of any kind. It is quite likely that such investors would not benefit much from TCP, and may even reduce their overall after-tax return.
If the low tax bracket is temporary, TCP over the long-term may still make sense. Also note that some combinations of account balances can, in certain circumstances, still add tax alpha for investors in low tax brackets. One example is when an investor only has traditional and Roth IRA accounts, and no taxable accounts being tax coordinated. Low bracket investors should very carefully consider whether TCP is suitable for them. As a general rule, we do not recommend it.
Potential Problems with Coordinating Accounts Meant for Different Time Horizons
We began with the premise that asset location is sensible only with respect to accounts that are generally intended for the same purpose. This is crucial, because unevenly distributing assets will result in asset allocations in each account that are not tailored towards the overall goal (or any goal at all). This is fine, as long as we expect that all coordinated accounts will be available for withdrawals at roughly the same time (e.g. at retirement). Only the aggregate portfolio matters in getting there.
However, uneven distributions are less diversified. Temporary drawdowns (e.g., the 2008 financial crisis) can mean that a single account may drop substantially more than the overall coordinated portfolio. If that account is intended for a short-term goal, it may not have a chance to recover by the time you need the money. Likewise, if you do not plan on depleting an account during your retirement, and instead plan on leaving it to be inherited for future generations, arguably this account has a longer time horizon than the others and should thus be invested more aggressively. In either case, we do not recommend managing accounts with materially different time horizons as a single portfolio.
For a similar reason, you should avoid applying asset location to an account that you expect will be long-term, but one that you may look to for emergency withdrawals. For example, a Safety Net Goal should never be managed by TCP.
Large Upcoming Transfers/Withdrawals
If you know you will be making large transfers in or out of your tax-coordinated accounts, you may want to delay enabling our tax coordination tool until after those transfers have occurred.
This is because large changes in the balances of the underlying accounts can necessitate rebalancing, and thus may cause taxes. With incoming deposits, we can intelligently rebalance your accounts by purchasing asset classes that are underweight. But when large withdrawals or transfers out are made, despite Betterment’s intelligent management of executing trades, some taxes can be unavoidable when rebalancing to your overall target allocation.
The only exception to this rule is if the large deposit will be in your taxable account instead of your IRAs. In that case, you should enable tax-coordination before depositing money into the taxable account. This is so our system knows to tax-coordinate you immediately.
The goal of tax coordination is to reduce the drag taxes have on your investments, not cause additional taxes. So if you know an upcoming withdrawal or outbound transfer could cause rebalancing, and thus taxes, it would be prudent to delay enabling tax coordination until you have completed those transfers.
Mitigating Behavioral Challenges Through Design
There is a broader issue that stems from locating assets with different volatility profiles at the account level, but it is behavioral. Uncoordinated portfolios with the same allocation move together. Asset location, on the other hand, will cause one account to dip more than another, testing an investor’s stomach for volatility. Those who enable TCP across their accounts should be prepared for such differentiated movements. Rationally, we should ignore this—after all, the overall allocation is the same—but that is easier said than done.
How TCP Interacts with Tax Loss Harvesting
TCP and TLH work in tandem, seeking to minimize tax impact. As described in more detail below, the precise interaction between the two strategies is highly dependent on personal circumstances. While it is possible that enabling a TCP may reduce harvest opportunities, both TLH and TCP derive their benefit without disturbing the desired asset allocation.
Operational Interaction
TLH was designed around a "tertiary ticker" system, which ensures that no purchase in an IRA or 401(k) managed by Betterment will interfere with a harvested loss in a Betterment taxable account.
A sale in a taxable account, and a subsequent repurchase of the same asset class in a qualified account would be incidental for accounts managed as separate portfolios. Under TCP, however, we expect this to occasionally happen by design. When "relocating" assets, either during initial setup, or as part of ongoing optimization, TCP will sell an asset class in one account, and immediately repurchase it in another. The tertiary ticker system allows this reshuffling to happen seamlessly, while attempting to protect any tax losses that are realized in the process.
Conceptualizing Blended Performance
TCP will affect the composition of the taxable account in ways that are hard to predict, because its decisions will be driven by changes in relative balances among the accounts. Meanwhile, the weight of specific asset classes in the taxable account is a material predictor of the potential value of TLH (more volatile assets should offer more harvesting opportunities). The precise interaction between the two strategies is far more dependent on personal circumstances, such as today’s account balance ratios and future cash flow patterns, than on generally applicable inputs like asset class return profiles and tax rules.
These dynamics are best understood as a hierarchy. Asset allocation comes first, and determines what mix of asset classes we should stick to overall. Asset location comes second, and continuously generates tax alpha across all coordinated accounts, within the constraints of the overall portfolio. Tax loss harvesting comes third, and looks for opportunities to generate tax alpha from the taxable account only, within the constraints of the asset mix dictated by asset location for that account.
TLH is usually most effective in the first several years after an initial deposit to a taxable account. Over decades, however, we expect it to generate value only from subsequent deposits and dividend reinvestments. Eventually, even a substantial dip is unlikely to bring the market price below the purchase price of the older tax lots. Meanwhile, TCP aims to deliver tax alpha over the entire balance of all three accounts for the entire holding period.
***
Betterment does not represent in any manner that TCP will result in any particular tax consequence or that specific benefits will be obtained for any individual investor. The TCP service is not intended as tax advice. Please consult your personal tax advisor with any questions as to whether TCP is a suitable strategy for you in light of your individual tax circumstances. Please see our Tax-Coordinated Portfolio Disclosures for more information.
Addendum
As of May 2020, for customers who indicate that they’re planning on using a Health Savings Account (HSA) for long-term savings, we allow the inclusion of their HSA in their Tax-Coordinated Portfolio.
If an HSA is included in a Tax-Coordinated Portfolio, we treat it essentially the same as an additional Roth account. This is because funds within an HSA grow income tax-free, and withdrawals can be made income tax-free for medical purposes. With this assumption, we also implicitly assume that the HSA will be fully used to cover long-term medical care spending.
The tax alpha numbers presented above have not been updated to reflect the inclusion of HSAs, but remain our best-effort point-in-time estimate of the value of TCP at the launch of the feature. As the inclusion of HSAs allows even further tax-advantaged contributions, we contend that the inclusion of HSAs is most likely to additionally benefit customers who enable TCP.
1"Boost Your After-Tax Investment Returns." Susan B. Garland. Kiplinger.com, April 2014.
2But see "How IRA Withdrawals In The Crossover Zone Can Trigger The 3.8% Medicare Surtax," Michael Kitces, July 23, 2014.
3It is worth emphasizing that asset location optimizes around account balances as it finds them, and has nothing to say about which account to fund in the first place. Asset location considers which account is best for holding a specified dollar amount of a particular asset. However, contributions to a TDA are tax-deductible, whereas getting a dollar into a taxable account requires more than a dollar of income.
4Pg. 5, The Kitces Report. January/February 2014.
5Daryanani, Gobind, and Chris Cordaro. 2005. "Asset Location: A Generic Framework for Maximizing After-Tax Wealth." Journal of Financial Planning (18) 1: 44–54.
6The Kitces Report, March/April 2014.
7While the significance of ordinary versus preferential tax treatment of income has been made clear, the impact of an individual’s specific tax bracket has not yet been addressed. Does it matter which ordinary rate, and which preferential rate is applicable, when locating assets? After all, calculating the after-tax return of each asset means applying a specific rate. It is certainly true that different rates should result in different after-tax returns. However, we found that while the specific rate used to derive the after-tax return can and does affect the level of resulting returns for different asset classes, it makes a negligible difference on resulting location decisions. The one exception is when considering using very low rates as inputs (the implication of which is discussed under "Special Considerations"). This should feel intuitive: Because the optimization is driven primarily by the relative size of the after-tax returns of different asset classes, moving between brackets moves all rates in the same direction, generally maintaining these relationships monotonically. The specific rates do matter a lot when it comes to estimating the benefit of the asset location chosen, so rate assumptions are laid out in the "Results" section. In other words, if one taxpayer is in a moderate tax bracket, and another in a high bracket, their optimal asset location will be very similar and often identical, but the high bracket investor may benefit more from the same location.
8In reality, the ordinary rate is applied to the entire value of the TDA, both the principal (i.e., the deductible contributions) and the growth. However, this will happen to the principal whether we use asset location or not. Therefore, we are measuring here only that which we can optimize.
9TCP today does not account for the potential benefit of a foreign tax credit (FTC). The FTC is intended to mitigate the potential for double taxation with respect to income that has already been taxed in a foreign country. The scope of the benefit is hard to quantify and its applicability depends on personal circumstances. All else being equal, we would expect that incorporating the FTC may somewhat increase the after-tax return of certain asset classes in a taxable account—in particular developed and emerging markets stocks. If maximizing your available FTC is important to your tax planning, you should carefully consider whether TCP is the optimal strategy for you.
10Standard market bid-ask spread costs will still apply. These are relatively low, as Betterment considers liquidity as a factor in its investment selection process. Betterment customers do not pay for trades.
11Additionally, in the interest of making interaction with the tool maximally responsive, certain computationally demanding aspects of the methodology were simplified for purposes of the tool only. This could result in a deviation from the target asset location imposed by the TCP service in an actual Betterment account.
12Another way to test performance is with a backtest on actual market data. One advantage of this approach is that it tests the strategy on what actually happened. Conversely, a forward projection allows us to test thousands of scenarios instead of one, and the future is unlikely to look like the past. Another limitation of a backtest in this context—sufficiently granular data for the entire Betterment portfolio is only available for the last 15 years. Because asset location is fundamentally a long-term strategy, we felt it was important to test it over 30 years, which was only possible with Monte Carlo. Additionally, Monte Carlo actually allows us to test tweaks to the algorithm with some confidence, whereas adjusting the algorithm based on how it would have performed in the past is effectively a type of "data snooping".
13That said, the strategy is expected to change the relative balances dramatically over the course of the period, due to unequal allocations. We expect a Roth balance in particular to eventually outpace the others, since the optimization will favor assets with the highest expected return for the TEA. This is exactly what we want to happen.
14For the uncoordinated taxable portfolio, we assume an allocation to municipal bonds (MUB) for the high-quality bonds component, but use investment grade taxable bonds (AGG) in the uncoordinated portfolio for the qualified accounts. While TCP makes use of this substitution, Betterment has offered it since 2014, and we want to isolate the additional tax alpha of TCP specifically, without conflating the benefits.
15Full liquidation of a taxable or TDA portfolio that has been growing for 30 years will realize income that is guaranteed to push the taxpayer into a higher tax bracket. We assume this does not happen, because in reality, a taxpayer in retirement will make withdrawals gradually. The strategies around timing and sequencing decumulation from multiple account types in a tax-efficient manner are out of scope for this paper.
Additional References
Berkin. A. "A Scenario Based Approach to After-Tax Asset Allocation." 2013. Journal of Financial Planning.
Jaconetti, Colleen M., CPA, CFP®. Asset Location for Taxable Investors, 2007. https://personal.vanguard.com/pdf/s556.pdf.
Poterba, James, John Shoven, and Clemens Sialm. "Asset Location for Retirement Savers." November 2000. https://faculty.mccombs.utexas.edu/Clemens.Sialm/PSSChap10.pdf.
Reed, Chris. "Rethinking Asset Location - Between Tax-Deferred, Tax-Exempt and Taxable Accounts." Accessed 2015. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2317970.
Reichenstein, William, and William Meyer. "The Asset Location Decision Revisited." 2013. Journal of Financial Planning 26 (11): 48–55.
Reichenstein, William. 2007. "Calculating After-Tax Asset Allocation is Key to Determining Risk, Returns, and Asset Location." Journal of Financial Planning (20) 7: 44–53.
